ホーム
> お知らせブログ - 銀天エコプラザ > 教育DXの一環としての、スパコンと線状降水帯のお話
| 日 | 月 | 火 | 水 | 木 | 金 | 土 |
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
宇部市環境学習ポータルサイト「うべっくる」では、山口県宇部市で行われる環境イベント情報を募集しています。環境イベントに関する情報はこちらからお知らせ下さい。
教育DXの一環としての、スパコンと線状降水帯のお話
2023年08月08日
山口県では地元の山口大学・山口県立大学・山口学芸大学が連携して文系DX人材育成プログラムが進められています。本プログラムの目的は、上記の3大学が、「地域社会と大学間の連携を通じて既存の教育プログラムを再構築し、地域をけん引する人材を育成する」ことであるとしています。この活動の一環として、今回、山口学芸大学教育学部の学生さんを対象にして、特別講義「スーパーコンピュータと計算科学による未来予測 ―線状降水帯の予測可能性についてー」を2023年8月4日に実施しました。参加学生22名、教職員4名、合計26名でした。
講義内容の概略は以下の通りです。
・計算科学は未来を予測できる科学です。
・台風の進路予測とか、線状降水帯の発生予測などは、空気の流れを支配する方程式をスパコンで解く必要があります。
・先ず聴講者の学生さんには支配方程式はどのようなものかを簡単にします。（文系の学生さんなので、理論の大枠のみを説明します）
・その支配方程式は、空間の何処でも成り立つので、対象とする地域の空間を細かい格子に分けます。各格子点において支配方程式が同時に成り立つので、格子点の数だけの支配方程式を同時に満足する解（連立方程式の解）を得る必要があります。
・ 例えば地球の赤道面を10kmの格子点で区切り、緯度・経度上で同数の区切り方をして、大気の厚さ方向には100分割すると合計16億個の格子点が出来ます。地球全体の気象予測（例えば将来の気候変動の予測）を行おうとすれば、この膨大な格子点における支配方程式を同時に解く必要があります。
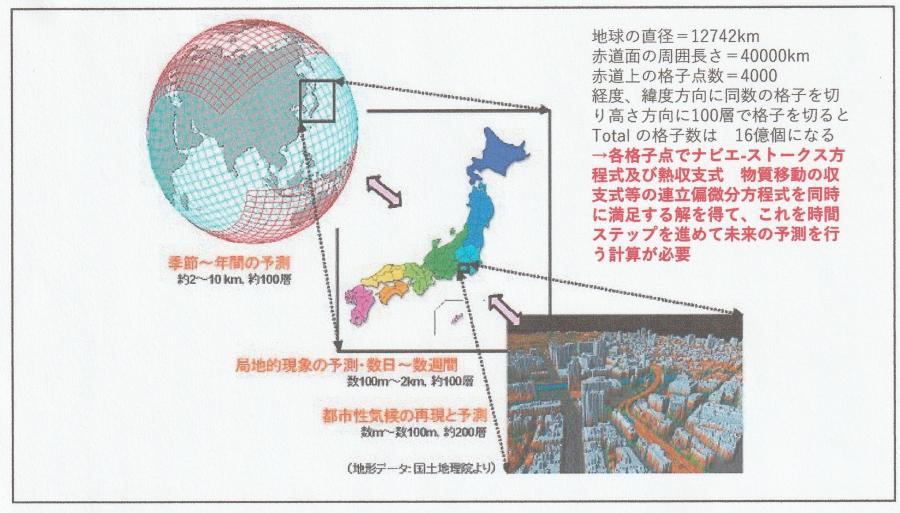
・台風や線状降水帯の予測は、もっと限定された領域について、格子点を形成して解くことになりますが、格子点の間隔はもっと短くする必要があり、望ましくは1km以下の格子間隔にする必要があります。また、集中豪雨による人家や都市への災害予測を行うためには、格子間隔は1m～100m程度に細かくする必要があります。
・何れにしても多数の連立方程式を解こうとすれば、高速・大容量の計算能力を有する計算機が必要であり、そのためにはスーパーコンピュータが必要になってくるのです。
・コンピュータの計算速度は、1秒間に15桁の数を例えば掛けたり割ったりすることが出来る回数で表します。通常のパソコンは1秒間に約1ギガ回の計算能力があり、スパコン「京」は毎秒1京回の計算能力がありました。現在日本の最速スパコンは「富岳」は京の約40倍（毎秒42.2京回）の計算能力があります。「富岳」は2021年に運用開始した時には世界一の計算速度を誇っていましたが、現在はUSAのオークリッジ国立研究所のスパコン「フロンティア」の毎秒119京回の計算速度が世界一になっています。
さて、当日の授業はニュートンの運動方程式から始めました。ニュートンは三代将軍家光の時代に生まれ、ケンブリッジ大学を1660年台に卒業して、20歳台で若さで万有引力の法則、ニュートンの運動方程式（ 力＝質量×加速度 ）を考えだしました。加速度は速度の変化率（毎秒その物体の速度が変化しているのかと言う変化率）です。授業では車に乗っている人がアクセルを踏んで、速度を増した時に感じる力だと説明しました。この力は受講者も理解できたと思われますが、上記の運動方程式で表した時に、どれだけの文系の学生さんが理解できたかは、心もとないところがあります
・ニュートンの時代から200年弱後の、江戸時代末期になると、ニュートンの運動方程式を空気とか水の流れに適用する一般式としてナビエさんとストークスさんが提案して、現在ナビエストークス方程式と呼ばれています。この式が大気の流れの中でどこでも成立することになります。
・先に述べた地球上の格子点について、ナビエストークス方程式が同時に成立するとして数十億個の格子点状の方程式をスパコンで解くことになります。
・大容量・並列計算の詳細は省きましたが、得られた解の例を台風進路や線状降水帯について示しました。細かい格子点で計算すると、より現実に近い予測結果が得られます。
（その２に続きます）
この記事のURL: http://ubekuru.com/blog_view.php?id=6058
◆ 現在、コメントはありません。
この記事へコメントを投稿します。